1.缺失值处理
1)常见的缺失值处理方法
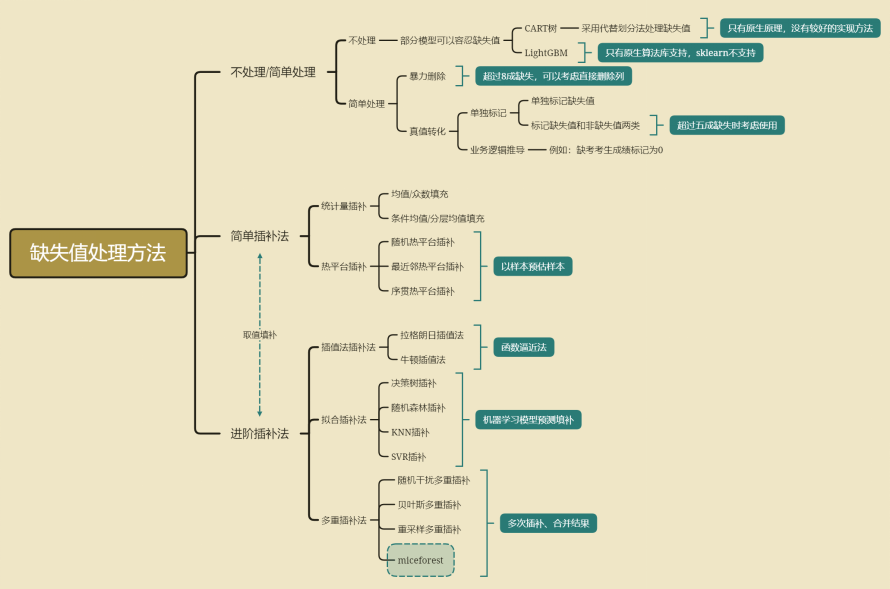
2)实际项目开发处理方法
少部分缺失,根据业务逻辑赋值,业务上认为应该填什么就填什么,业务上能解释
少部分缺失,二分类问题,离散变量处理,基于业务逻辑根据Bad Rate大小,把和缺失值和非缺失值Bad Rate差不多的归为一类
少部分缺失,二分类问题,连续变量处理,先使用最大KS分箱或卡方分箱或业务逻辑分箱,在把缺失值和非缺失值箱体Bad Rate差不多的归为一类。
缺失值的分箱归类,主要还是看分箱是否符合业务逻辑,如果这个变量无法在合理的业务逻辑上进行分箱并获得客观的Bad Rate,最好将这个变量删除
超过八成缺失,直接删除
超过五成缺失,标记为缺失值和非缺失值两类,主要看变量价值(例如IV值),把null当成一种取值看待。
除非对业务完全不理解,否则不建议使用众数、均值等方法直接填充
def missing (df): """ 计算每一列的缺失值及占比 """ missing_number = df.isnull().sum().sort_values(ascending=False) # 每一列的缺失值求和后降序排序 missing_percent = (df.isnull().sum()/df.isnull().count()).sort_values(ascending=False) # 每一列缺失值占比 missing_values = pd.concat([missing_number, missing_percent], axis=1, keys=['Missing_Number', 'Missing_Percent']) # 合并为一个DataFramereturn missing_values
2.数据编码
清洗完后的数据需要进行进一步重编码后才能带入进行建模
快速验证不同模型的建模效果时,需要考虑到不同模型对数据编码要求是不同的,
因此我们需要进行特征编码
1)离散变量重编码
不同类型的字段由不同的编码方式,例如文本类型字段可能需要用到CountVector或TF-IDF处理、时序字段可能需要分段字典排序等
并且,不同模型对于数据编码类型要求也不一样,例如逻辑回归需要对多分类离散变量进行线性变换。
对于二分类离散变量来说,独热编码往往是没有实际作用的。进行独热编码转化的时候会考虑只对多分类离散变量进行转化,而保留二分类离散变量
#--------------------------------------独热编码 开始------------------------------------ from sklearn.preprocessing import LabelEncoder,OneHotEncoder def cate_colName(Transformer, category_cols, drop='if_binary'): """ 离散字段独热编码后字段名创建函数 :param Transformer: 独热编码转化器 :param category_cols: 输入转化器的离散变量 :param drop: 独热编码转化器的drop参数 """ cate_cols_new = [] col_value = Transformer.categories_ # 查看one-hot 列的值 for i, j in enumerate(category_cols): if (drop == 'if_binary') & (len(col_value[i]) == 2): cate_cols_new.append(j) else: for f in col_value[i]: feature_name = j + '_' + f cate_cols_new.append(feature_name) return(cate_cols_new) # 对 tcc 数据集进行多分类转化 enc = OneHotEncoder(drop='if_binary') # 离散字段单独为一个数据集 df_cate = tcc[category_cols] # one-hot转化 enc.fit(df_cate) # one-hot转化后的,离散数据集 pd.DataFrame(enc.transform(df_cate).toarray(), columns=cate_colName(enc, category_cols))
最后说明,非必要,不用one-hot。个人理解是,增加了特征维度,但又没有增加特征的信息量。
模型的拟合能力来源于单个变量对Y的拟合能力和变量个数,每增加一个变量就增加一维,能增加模型的拟合能力,又由于独热编码产生的单个变量包含的信息量少
于是乎就会造成,模型过拟合,但是预测效果又不好情况。
2)连续变量分箱
在实际模型训练过程中,经常需要对连续型字段进行离散化处理,也就是将连续性字段转化为离散型字段。
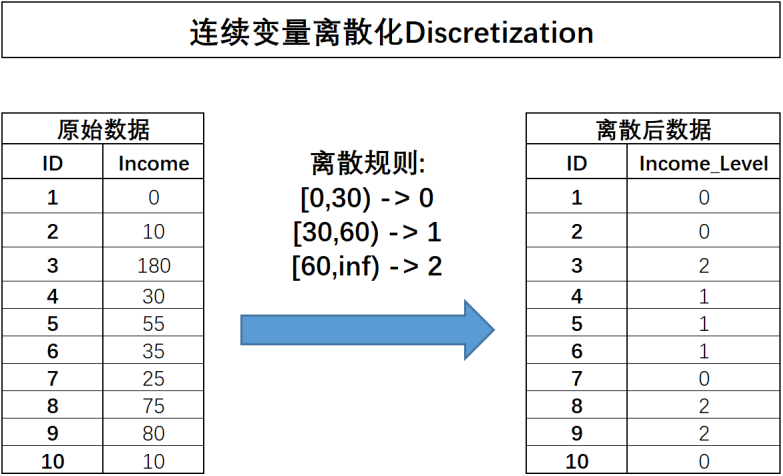
离散之后字段的含义将发生变化,原始字段Income代表用户真实收入状况,而离散之后的含义就变成了用户收入的等级划分,0表示低收入人群、1表示中等收入人群、2代表高收入人群。
连续字段的离散化能够更加简洁清晰的呈现特征信息,并且能够极大程度减少异常值的影响(例如Income取值为180的用户),同时也能够消除特征量纲影响,当然,最重要的一点是,对于很多线性模型来说,连续变量的分箱实际上相当于在线性方程中引入了非线性的因素,从而提升模型表现。
当然,连续变量的分箱过程会让连续变量损失一些信息(降低了求解的精度),而对于其他很多模型来说(例如树模型),分箱损失的信息则大概率会影响最终模型效果。
对于特定的数据集, 如果有充分的理由使用线性模型, 比如数据集很大或维度很高时, 但有些特征的输入和输出关系是非线性的, 那么分箱( 离散化 )是提高建模能力的好方法。使用Bad Rate方法,也能将非线性的连续变量,通过业务逻辑,按照Bad Rate大小,分箱成线性关系
3)分箱说明
(1)业务指标确定
有明确业务背景的场景中,或许能够找到一些根据长期实践经验积累下来的业务指标来作为划分依据,例如很多金融行业会通过一些业务指标来对用户进行价值划分,例如会规定月收入10000以上属于高收入人群,此时10000就可以作为连续变量离散化的依据。
(2)常见分箱方法
更常见的一种情况是并没有明确的业务指标作为划分依据,此时我们就需要通过某种计算流程来进行确定。常见方法有四种,分别是等宽分箱(等距分箱)、等频分箱(等深分箱)、聚类分箱和有监督分箱
等宽、等频分箱基本不用于项目开发,原因是等宽分箱会一定程度受到异常值的影响,而等频分箱又容易完全忽略异常值信息,从而一定程度上导致特征信息损失,而若要更好的兼顾变量原始数值分布,则可以考虑使用聚类分箱
(3)聚类分箱
先对某连续变量进行聚类(往往是KMeans聚类),然后用样本所属类别作为标记代替原始数值,从而完成分箱的过程。
# 转化为列向量 income = np.array([0, 10, 180, 30, 55, 35, 25, 75, 80, 10]).reshape(-1, 1) # 一列特征必须以列向量呈现,才能够被KBinsDiscretizer正确识别 from sklearn import cluster kmeans = cluster.KMeans(n_clusters=3) kmeans.fit(income) # 训练评估器 kmeans.labels_ # 通过.labels_查看每条样本所属簇的类别
4)有监督分箱
最大KS分箱
from sklearn.metrics import roc_curve
import numpy as np
import pandas as pd
# 将类别转为类别矩阵(one-hot格式)
def class2Cmat(y):
c_name = list(np.unique(y)) # 类别名称
c_num = len(c_name) # 类别个数
cMat = np.zeros([len(y),c_num]) # 初始化类别矩阵
for i in range(c_num):
cMat[y==c_name[i],i] = 1 # 将样本对应的类别标为1
c_name = [str(i) for i in c_name] # 类别名称统一转为字符串类型
return cMat,c_name # 返回one-hot类别矩阵和类别名称
# 将切割点转换成分箱说明
def getBinDesc(bin_cut):
# 分箱说明
bin_first = ['<='+str(bin_cut[0])] # 第一个分箱
bin_last = ['>'+str(bin_cut[-1])] # 最后一个分箱
bin_desc = ['('+str(bin_cut[i])+','+str(bin_cut[i+1])+']' for i in range(len(bin_cut)-1)]
bin_desc = bin_first+bin_desc+bin_last # 分箱说明
return bin_desc
# 计算分箱详情
def statBinNum(x,y,bin_cut):
if(len(bin_cut)==0): # 如果没有切割点
return None # 返回空
bin_desc = getBinDesc(bin_cut) # 获取分箱说明
c_mat,c_name = class2Cmat(y) # 将类别转为one-hot类别矩阵
df = pd.DataFrame(c_mat,columns=c_name,dtype=int) # 将类别矩阵转为dataFrame
df['cn'] = 1 # 预设一列1,方向后面统计
df['grp'] = 0 # 初始化分组序号
df['grp_desc'] = '' # 初始化分箱说明
# 计算各个样本的分组序号与分箱说明
df.loc[x<=bin_cut[0],'grp']=0 # 第0组样本的序号
df.loc[x<=bin_cut[0],'grp_desc'] =bin_desc[0] # 第0组样本的分箱说明
for i in range(len(bin_cut)-1): # 逐区间计算分箱序号与分箱说明
df.loc[(x>bin_cut[i])&(x<=bin_cut[i+1]),'grp'] =i+1
df.loc[(x>bin_cut[i])&(x<=bin_cut[i+1]),'grp_desc'] =bin_desc[i+1]
df.loc[x>bin_cut[-1],'grp']=len(bin_cut) # 最后一组样本的序号
df.loc[x>bin_cut[-1],'grp_desc']=bin_desc[-1] # 最后一组样本的分箱说明
# 按组号聚合,统计出每组的总样本个数和各类别的样本个数
col_dict = {'grp':'max','grp_desc':'max','cn':'sum'}
col_dict.update({col:'sum' for col in c_name})
df = df.groupby('grp').agg(col_dict).reset_index(drop=True)
return df
#---------------------以上部分只用于统计分箱结果详情,与KS分箱算法无关-----------------------
# 获取ks切割点
def getKsCutPoint(x,y):
fpr, tpr, thresholds= roc_curve(y, x) # 计算fpr,tpr
ks_idx = np.argmax(abs(fpr-tpr)) # 计算最大ks所在位置
#由于roc_curve给出的切割点是>=作为右箱,而我们需要的是>作为右箱,所以切割点应向下再取一位,也即索引向上取一位
return thresholds[ks_idx+1] # 返回切割点
# 检查切割点是否有效
def checkCutValid(x,y,cutPoint,woe_asc,min_sample):
left_y = y[x<=cutPoint] # 左箱的y
right_y = y[x>cutPoint] # 右箱的y
check_sample_num = min(len(left_y),len(right_y))>=min_sample # 检查左右箱样本是否足够
left_rate = sum(left_y)/max((len(left_y)-sum(left_y)),1) # 左箱好坏比例
right_rate = sum(right_y)/max((len(right_y)-sum(right_y)),1) # 右箱好坏比例
cur_woe_asc = left_rate<right_rate # 通过好坏比例的比较,确定woe是否上升
check_woe_asc = True if woe_asc ==None else cur_woe_asc == woe_asc # 检查woe方向是否与预期一致
woe_asc = cur_woe_asc if woe_asc ==None else woe_asc # 首次woe方向为空,需要返回woe方向
cut_valid = check_sample_num & check_woe_asc # 样本足够且woe方向正确,则本次切割有效
return cut_valid,woe_asc
# 获取箱体切割点
def cutBin(bin_x,bin_y,woe_asc,min_sample):
cutPoint = getKsCutPoint(bin_x,bin_y) # 获取最大KS切割点
is_cut_valid,woe_asc = checkCutValid(bin_x,bin_y,cutPoint,woe_asc,min_sample) # 检查切割点是否有效
if( not is_cut_valid): # 如果切割点无效
cutPoint = None # 返回None
return cutPoint,woe_asc # 返回切割点
# 检查箱体是否不需再分
def checkBinFinish(y,min_sample):
check_sample_num = len(y)<min_sample # 检查样本是否足够
check_class_pure = (sum(y) == len(y))| (sum(y) == 0) # 检查样本是否全为一类
bin_finish = check_sample_num | check_class_pure # 如果样本足够或者全为一类,则不需再分
return bin_finish
# KS分箱主流程
def ksMerge(x,y,min_sample,max_bin):
# -----初始化分箱列表等变量----------------
un_cut_bins = [[min(x)-0.1,max(x)]] # 初始化待分箱列表
finish_bins = [] # 初始化已完成分箱列表
woe_asc = None # 初始化woe方向
# -----如果待分箱体不为空,则对待分箱进行分箱----------------
for i in range(10000): # 为避免有bug使用while不安全,改为for
cur_bin = un_cut_bins.pop(0) # 从待分箱列表获取一个分箱
bin_x = x[(x>cur_bin[0])&(x<=cur_bin[1])] # 当前分箱的x
bin_y = y[(x>cur_bin[0])&(x<=cur_bin[1])] # 当前分箱的y
cutPoint,woe_asc = cutBin(bin_x,bin_y,woe_asc,min_sample) # 获取分箱的最大KS切割点
if (cutPoint==None): # 如果切割点无效
finish_bins.append(cur_bin) # 将当前箱移到已完成列表
else: # 如果切割点有效
# ------检查左箱是否需要再分,需要再分就添加到待分箱列表,否则添加到已完成列表-----
left_bin = [cur_bin[0],cutPoint] # 生成左分箱
left_y = bin_y[bin_x <=cutPoint] # 获取左箱y数据
left_finish = checkBinFinish(left_y,min_sample) # 检查左箱是否不需再分
if (left_finish): # 如果左箱不需再分
finish_bins.append(left_bin) # 将左箱添加到已完成列表
else: # 否则
un_cut_bins.append(left_bin) # 将左箱移到待分箱列表
# ------检查右箱是否需要再分,需要再分就添加到待分箱列表,否则添加到已完成列表-----
right_bin = [cutPoint,cur_bin[1]] # 生成右分箱
right_y = bin_y[bin_x >cutPoint] # 获取右箱y数据
right_finish = checkBinFinish(right_y,min_sample) # 检查右箱是否不需再分
if (right_finish): # 如果右箱不需再分
finish_bins.append(right_bin) # 将右箱添加到已完成列表
else: # 否则
un_cut_bins.append(right_bin) # 将右箱移到待分箱列表
# 检查是否满足退出分箱条件:待分箱列表为空或者分箱数据足够
if((len(un_cut_bins)==0)|((len(un_cut_bins)+len(finish_bins))>=max_bin)):
break
# ------获取分箱切割点-------
bins = un_cut_bins + finish_bins # 将完成或待分的分箱一起作为最后的分箱结果
bin_cut = [cur_bin[1] for cur_bin in bins] # 获取分箱右边的值
list.sort(bin_cut) # 排序
bin_cut.pop(-1) # 去掉最后一个,就是分箱切割点
# ------------分箱说明--------------
bin_desc ='['+str(min(x))+','+str(max(x))+']' # 如果没有切割点,就只有一个分箱[min_x,max_x]
if (len(bin_cut)>0) : # 如果有切割点
bin_desc = getBinDesc(bin_cut) # 获取分箱说明
# ------------返回结果--------------
return bin_cut,bin_desc卡方分箱
import numpy as np
import pandas as pd
import scipy
# 将类别转为类别矩阵(one-hot格式)
def class2Cmat(y):
c_name = list(np.unique(y)) # 类别名称
c_num = len(c_name) # 类别个数
cMat = np.zeros([len(y),c_num]) # 初始化类别矩阵
for i in range(c_num):
cMat[y==c_name[i],i] = 1 # 将样本对应的类别标为1
c_name = [str(i) for i in c_name] # 类别名称统一转为字符串类型
return cMat,c_name # 返回one-hot类别矩阵和类别名称
# 将切割点转换成分箱说明
def getBinDesc(bin_cut): # 特征数据过于集中,会导致这里分箱数不够10个
# 分箱说明
bin_first = ['<='+str(bin_cut[0])] # 第一个分箱
bin_last = ['>'+str(bin_cut[-1])] # 最后一个分箱
bin_desc = ['('+str(bin_cut[i])+','+str(bin_cut[i+1])+']' for i in range(len(bin_cut)-1)]
bin_desc = bin_first+bin_desc+bin_last # 分箱说明
return bin_desc
# 计算分箱详情
def statBinNum(x,y,bin_cut):
if(len(bin_cut)==0): # 如果没有切割点
return None # 返回空
bin_desc = getBinDesc(bin_cut) # 获取分箱说明,#特征数据过于集中,会导致这里分箱数不够10个这里就报错
c_mat,c_name = class2Cmat(y) # 将类别转为one-hot类别矩阵
df = pd.DataFrame(c_mat,columns=c_name,dtype=int) # 将类别矩阵转为dataFrame
df['cn'] = 1 # 预设一列1,方向后面统计
df['grp'] = 0 # 初始化分组序号
df['grp_desc'] = '' # 初始化分箱说明
# 计算各个样本的分组序号与分箱说明
df.loc[x<=bin_cut[0],'grp']=0 # 第0组样本的序号
df.loc[x<=bin_cut[0],'grp_desc'] =bin_desc[0] # 第0组样本的分箱说明
for i in range(len(bin_cut)-1): # 逐区间计算分箱序号与分箱说明
df.loc[(x>bin_cut[i])&(x<=bin_cut[i+1]),'grp'] =i+1
df.loc[(x>bin_cut[i])&(x<=bin_cut[i+1]),'grp_desc'] =bin_desc[i+1]
df.loc[x>bin_cut[-1],'grp']=len(bin_cut) # 最后一组样本的序号
df.loc[x>bin_cut[-1],'grp_desc']=bin_desc[-1] # 最后一组样本的分箱说明
# 按组号聚合,统计出每组的总样本个数和各类别的样本个数
col_dict = {'grp':'max','grp_desc':'max','cn':'sum'}
col_dict.update({col:'sum' for col in c_name})
df = df.groupby('grp').agg(col_dict).reset_index(drop=True)
return df
# 初始化分箱
'''
按等频分箱,等频分箱并不代表每个箱里的样本个数都一样,
因为如果每10个样本作为一个箱,刚好9-11样本的x取值一样,
那必须把9-11划到同一个箱。
'''
def initBin(x,y,bin_num=10): #特别注意,这里,等频率分箱,原始数据过于集中,会导致,分箱分不开
xx = x.copy()
xx.sort()
idx = [int(np.floor((len(x)/bin_num)*(i+1))-1) for i in range(bin_num-1)]
bin_cut = list(xx[idx])
return bin_cut
#计算卡方值
def cal_chi2(pair):
# chi2_value,p,free_n,ex = scipy.stats.chi2_contingency(pair)
pair[pair==0] = 1
class_rate = pair.sum(axis=1)/pair.sum().sum() # 两类样本的占比
col_sum = pair.sum(axis=0) # 各组别的样本个数
ex = np.dot(np.array([class_rate]).T,np.array([col_sum])) # 计算期望值
chi2 = (((pair - ex)**2/ex)).sum() # 计算卡方值
return chi2
# 计算P值
def cal_p(df):
chi2_list = [cal_chi2(np.array(df.iloc[i:i+2,:])) for i in range(df.shape[0]-1)] # 计算卡方值
grp_num = df.shape[1] # 计算组别个数
free_n = grp_num - 1 # 计算自由度
p_list = [1-scipy.stats.chi2.cdf(df=free_n, x=i) for i in chi2_list] # 计算p值
return p_list
# 卡方分箱主函数,bin_desc为分组说明
def Chi2Merge(x,y,bin_num = 5,init_bin_num=10):
# ------------初始化--------------------------------
bin_cut = initBin(x,y,bin_num=init_bin_num) # 初始化分箱
df = statBinNum(x,y,bin_cut)
df.drop(columns = ['cn'])
bin_cut.append(max(x))
df['grp_desc'] = bin_cut
c_name = list(np.unique(y))
c_name = [str(i) for i in c_name]
# ------------根据卡方值合并分箱,直到达到目标分箱数---------------------
while(df.shape[0]>bin_num):
# 计算卡方值
chi2_list = [cal_chi2(np.array(df[c_name][i:i+2])) for i in range(df.shape[0]-1)]
#将卡方值最小的两组合并
min_idx = np.argmin(chi2_list)
df.loc[min_idx+1,c_name] += df.loc[min_idx,c_name]
df.drop(min_idx, inplace = True)
df = df.reset_index(drop=True)
# ----------输出结果-----------------------------
bin_cut = list(df['grp_desc'][:-1]) # 获取切割点
bin_desc = getBinDesc(bin_cut) # 获取分箱说明
return bin_cut,bin_desc5)分箱必要性
建立分类模型时,需要对连续变量离散化,特征离散化后,模型会更稳定,降低了模型过拟合的风险
如在建立申请评分卡模型时用logsitic作为基模型就需要对连续变量进行离散化,离散化通常采用分箱法
在银行评分卡的项目中,通常都会需要把数据分箱,分箱后并不是对数据进行WOE值替换,再放入模型
离散特征的类别进行分箱二次分类(比如,中国的所有城市,通过分箱划分为县区市地区等),易于模型的快速迭代;
稀疏向量内积乘法运算速度快,计算结果方便存储,容易扩展;
对于连续特征,分箱会降低数据的噪声影响。分箱后的数据有很强的稳定性。比如一个特征是年龄>30是1,否则0。如果特征没有离散化,一个异常数据“年龄300岁”会给模型造成很大的干扰;
特征离散化后,模型会更稳定,比如如果对用户年龄离散化,20-30作为一个区间,不会因为一个用户年龄长了一岁就变成一个完全不同的人;
特征离散化以后,起到了简化了逻辑回归模型的作用,降低了模型过拟合的风险;
可以将缺失作为独立的一类带入模型。
3.分组统计特征衍生策略
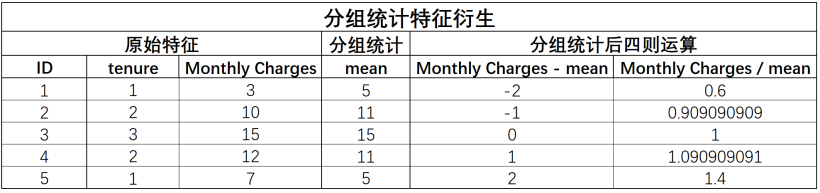
一种同样非常常用的特征衍生方法,A特征根据B特征的不同取值进行分组统计,统计量可以是均值、方差等针对连续变量的统计指标,也可以是众数、分位数等针对离散变量的统计指标
例如我们可以计算不同入网时间用户的平均月消费金额、消费金额最大值、消费金额最小值等,基本过程如下:
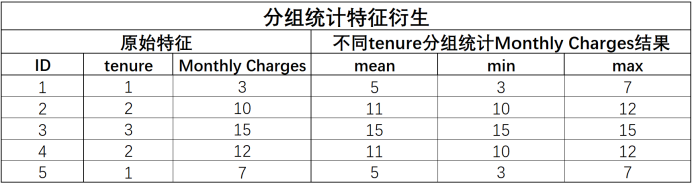
1)注意事项
A特征可以是离散变量也可以是连续变量,而B特征必须是离散变量,且最好是一些取值较多的离散变量(或者固定取值的连续变量),例如本数据集中的tenure字段,总共有73个取值。主要原因是如果B特征取值较少,则在衍生的特征矩阵中会出现大量的重复的行;
计算A的分组统计量时,可以不局限于连续特征只用连续变量的统计量、离散特征只用离散的统计量,完全可以交叉使用,例如A是离散变量,我们也可以分组统计其均值、方差、偏度、峰度等,连续变量也可以统计众数、分位数等。很多时候,更多的信息组合有可能会带来更多的可能性;
分组统计还可以用于多表连接的场景,例如假设现在给出的数据集不是每个用户的汇总统计结果,而是每个用户在过去的一段时间内的行为记录,则我们可以根据用户ID对其进行分组统计汇总:
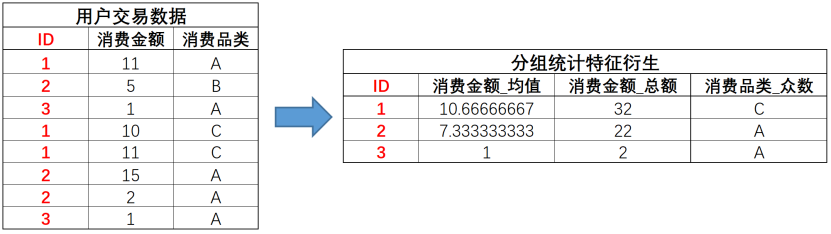
虑进一步围绕特征A和分组统计结果进行再一次的四则运算特征衍生,例如用月度消费金额减去分组均值,则可以比较每一位用户与相同时间入网用户的消费平均水平的差异,围绕衍生特征再次进行衍生,我们将其称为统计演变特征,也是分组汇总衍生特征的重要应用场景:
2)分组统计函数封装代码
def Binary_Group_Statistics(keyCol,
features,
col_num=None,
col_cat=None,
num_stat=['mean', 'var', 'max', 'min', 'skew', 'median'],
cat_stat=['mean', 'var', 'max', 'min', 'median', 'count', 'nunique'],
quant=True):
"""
双变量分组统计特征衍生函数
:param keyCol: 分组参考的关键变量
:param features: 原始数据集
:param col_num: 参与衍生的连续型变量
:param col_cat: 参与衍生的离散型变量
:param num_stat: 连续变量分组统计量
:param cat_num: 离散变量分组统计量
:param quant: 是否计算分位数
:return:交叉衍生后的新特征和新特征的名称
"""
# 当输入的特征有连续型特征时
if col_num != None:
aggs_num = {}
colNames = col_num
# 创建agg方法所需字典
for col in col_num:
aggs_num[col] = num_stat
# 创建衍生特征名称列表
cols_num = [keyCol]
for key in aggs_num.keys():
cols_num.extend([key+'_'+keyCol+'_'+stat for stat in aggs_num[key]])
# 创建衍生特征df
features_num_new = features[col_num+[keyCol]].groupby(keyCol).agg(aggs_num).reset_index()
features_num_new.columns = cols_num
# 当输入的特征有连续型也有离散型特征时
if col_cat != None:
aggs_cat = {}
colNames = col_num + col_cat
# 创建agg方法所需字典
for col in col_cat:
aggs_cat[col] = cat_stat
# 创建衍生特征名称列表
cols_cat = [keyCol]
for key in aggs_cat.keys():
cols_cat.extend([key+'_'+keyCol+'_'+stat for stat in aggs_cat[key]])
# 创建衍生特征df
features_cat_new = features[col_cat+[keyCol]].groupby(keyCol).agg(aggs_cat).reset_index()
features_cat_new.columns = cols_cat
# 合并连续变量衍生结果与离散变量衍生结果
df_temp = pd.merge(features_num_new, features_cat_new, how='left',on=keyCol)
features_new = pd.merge(features[keyCol], df_temp, how='left',on=keyCol)
features_new.loc[:, ~features_new.columns.duplicated()]
colNames_new = cols_num + cols_cat
colNames_new.remove(keyCol)
colNames_new.remove(keyCol)
# 当只有连续变量时
else:
# merge连续变量衍生结果与原始数据,然后删除重复列
features_new = pd.merge(features[keyCol], features_num_new, how='left',on=keyCol)
features_new.loc[:, ~features_new.columns.duplicated()]
colNames_new = cols_num
colNames_new.remove(keyCol)
# 当没有输入连续变量时
else:
# 但存在分类变量时,即只有分类变量时
if col_cat != None:
aggs_cat = {}
colNames = col_cat
for col in col_cat:
aggs_cat[col] = cat_stat
cols_cat = [keyCol]
for key in aggs_cat.keys():
cols_cat.extend([key+'_'+keyCol+'_'+stat for stat in aggs_cat[key]])
features_cat_new = features[col_cat+[keyCol]].groupby(keyCol).agg(aggs_cat).reset_index()
features_cat_new.columns = cols_cat
features_new = pd.merge(features[keyCol], features_cat_new, how='left',on=keyCol)
features_new.loc[:, ~features_new.columns.duplicated()]
colNames_new = cols_cat
colNames_new.remove(keyCol)
if quant:
# 定义四分位计算函数
def q1(x):
"""
下四分位数
"""
return x.quantile(0.25)
def q2(x):
"""
上四分位数
"""
return x.quantile(0.75)
aggs = {}
for col in colNames:
aggs[col] = ['q1', 'q2']
cols = [keyCol]
for key in aggs.keys():
cols.extend([key+'_'+keyCol+'_'+stat for stat in aggs[key]])
aggs = {}
for col in colNames:
aggs[col] = [q1, q2]
features_temp = features[colNames+[keyCol]].groupby(keyCol).agg(aggs).reset_index()
features_temp.columns = cols
features_new = pd.merge(features_new, features_temp, how='left',on=keyCol)
features_new.loc[:, ~features_new.columns.duplicated()]
colNames_new = colNames_new + cols
colNames_new.remove(keyCol)
features_new.drop([keyCol], axis=1, inplace=True)
return features_new, colNames_new4.时序特征衍生
使用一类仅仅通过时序特征就能够对标签进行预测的模型——时间序列模型
关于时序字段的展示形式,时序字段往往记录的就是时间是真实时间,并且是精确到年-月-日、甚至是小时-分钟-秒的字段,例如"2022-07-01;14:22:01",此时拿到数据后,首先需要考虑的是如何对这类字段进行处理。
一般来说时间字段的记录格式都是用'-'来划分年月日,用':'来分割时分秒,用空格、分号或者换行来分割年月日与时分秒,这是一种通用的记录方法,如果是手动输入时间,也尽可能按照上述格式进行记录
除了用不同的列记录时序字段的年月日、时分秒之外,还有一些自然周期也会对结果预测有较大影响,如日期所在季度。
这里需要注意的是,对于时序字段,往往我们会尽可能的对其进行自然周期的划分,然后在后续进行特征筛选时再对这些衍生字段进行筛选,
对于此前的数据集,我们能够清晰的看到季度特征对标签的影响,而很多时候,除了季度,诸如全年的第几周、一周的第几天,甚至是日期是否在周末,
具体事件的时间是在上午、下午还是在晚上等,都会对预测造成影响。
对于这些自然周期提取方法,有些自然周期可以通过dt的方法自动计算,另外则需要手动进行计算。首先我们先看能够自动完成计算的自然周期:
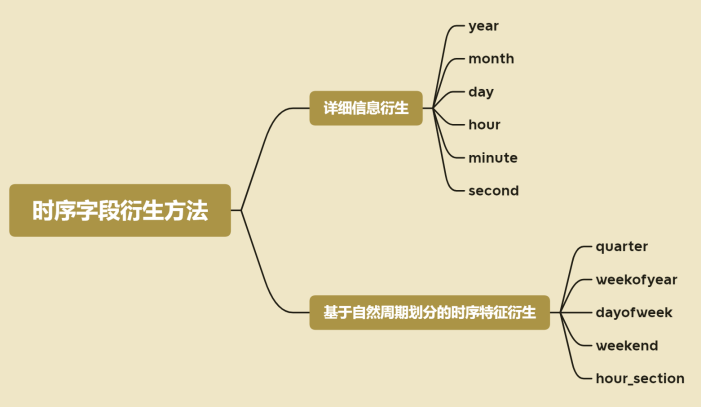
1)时序字段特征衍生的本质-增加分组
时序字段衍生的本质:增加分组
在tenure时序特征进行特征衍生后,ID1-6号用户在所属年份列中就被划分到了2019年组中,即他们同为2019年入网的用户,而根据入网的季节进行划分,则ID为0、4、5的三个用户会被划归到第一季度入网用户组中,并且时序特征衍生的字段越多、对用户分组的维度也就越多:
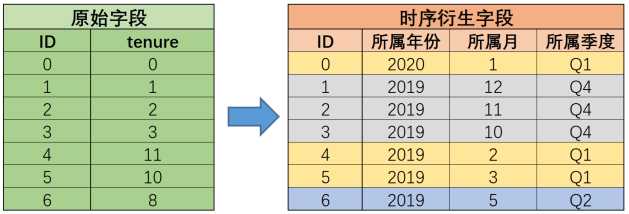
而对用户进行分组之所以能够帮助模型进行建模与训练,其根本原因也是因为有的时候,同一组内的用户会表现出相类似的特性(或者规律),从而能够让模型更快速的对标签进行更准确的预测
例如假设数据集如下所示,在原始数据集看来,标签取值毫无规律可言,但当我们对其进行时序特征的特征衍生后,立刻能发掘很多规律,例如第四季度用户都流失了、其二是2019年第一季度用户流失都流失了等等,同样,这些通过观察就能看到的规律,也很快会被模型捕捉到,而这也是时序字段衍生能够帮助模型进行更好更快的预测的直观体现:
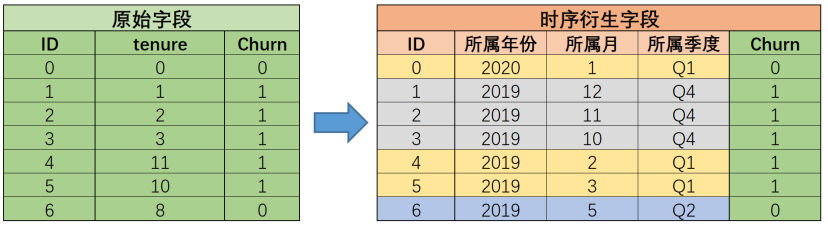
很多时候也是因为我们不知道什么样的分组能够有效的帮助到模型进行建模,因此往往需要衍生尽可能多的字段,来进行尽可能多的分组,而这些时序字段的衍生字段,也会在后续的建模过程中接受特征筛选的检验。
2)时序字段衍生的核心思路-自然周期和业务周期
在进行了细节时间特征的衍生之后(划分了年月日、时分秒之后),接下来的时序特征衍生就需要同时结合自然周期和业务周期两个方面进行考虑
自然周期,指的是对于时间大家普遍遵照或者约定俗成的一些规定,例如工作日周末、一周七天、一年四个季度等,这也就是此前我们进行的一系列特征衍生工作,此外其实还可以根据一些业务周期来进行时序特征的划分,例如对于部分旅游景点来说,暑假是旅游旺季,并且很多是以家庭为单位进行出游(学生暑假),因此可以考虑单独将8、9月进行标记,期间记录的用户会有许多共性,而组内用户的共性就将成为后续建模效果的保障;再比如6月、11月是打折季,也可以类似的单独设一列对6月、11月进行标记等等,这些需要特征的衍生,则需要结合具体业务情况来进行判断。
如果我们判断新衍生的特征在对数据分组的过程中, 不同组的数据在标签分布上并没有差别,则分组无效,我们大可不必进行如此特征衍生。
例如,对于一家普通电商平台用户交易时间的秒和分,从业务角度出发,我们很难说每分钟第一秒交易的用户有哪些共同的特点,或者每小时第二分钟交易的用户有哪些共同的特点,甚至是每分钟的前30秒用户有哪些共同特点、每小时的前半个小时用户呈现出哪些共同的特点等,而这类特征就不必在衍生过程中进行创建了。
但是,在另外一些场景下,例如某线下超市的周五,可能就是一个需要重点关注的时间,不仅是因为临近周末很多客户会在下班后进行集中采购、而且很多超市有“黑五”打折的习惯,如果是进行超市销售额预测,是否是周五可能就需要单独标注出来,形成独立的一列(该列被包含在dayofweek的衍生列中)。
总结来看,一方面,我们需要从自然周期和业务周期两个角度进行尽可能多的特征衍生,来提供更多的备选数据分组依据来辅助模型建模,而另一方当面,我们有需要结合当前实际业务情况来判断哪些时序特征的衍生特征是有效的,提前规避掉一些可能并无太大用处的衍生特征。
3)时序衍生特征函数封装代码
def timeSeriesCreation(timeSeries, timeStamp=None, precision_high=False):
"""
时序字段的特征衍生
:param timeSeries:时序特征,需要是一个Series
:param timeStamp:手动输入的关键时间节点的时间戳,需要组成字典形式,字典的key、value分别是时间戳的名字与字符串
:param precision_high:是否精确到时、分、秒
:return features_new, colNames_new:返回创建的新特征矩阵和特征名称
"""
# 创建衍生特征df
features_new = pd.DataFrame()
# 提取时间字段及时间字段的名称
timeSeries = pd.to_datetime(timeSeries)
colNames = timeSeries.name
# 年月日信息提取
features_new[colNames+'_year'] = timeSeries.dt.year
features_new[colNames+'_month'] = timeSeries.dt.month
features_new[colNames+'_day'] = timeSeries.dt.day
if precision_high != False:
features_new[colNames+'_hour'] = timeSeries.dt.hour
features_new[colNames+'_minute'] = timeSeries.dt.minute
features_new[colNames+'_second'] = timeSeries.dt.second
# 自然周期提取
features_new[colNames+'_quarter'] = timeSeries.dt.quarter
features_new[colNames+'_weekofyear'] = timeSeries.dt.isocalendar().week
features_new[colNames+'_dayofweek'] = timeSeries.dt.dayofweek + 1
features_new[colNames+'_weekend'] = (features_new[colNames+'_dayofweek'] > 5).astype(int)
if precision_high != False:
features_new['hour_section'] = (features_new[colNames+'_hour'] // 6).astype(int)
# 关键时间点时间差计算
# 创建关键时间戳名称的列表和时间戳列表
timeStamp_name_l = []
timeStamp_l = []
if timeStamp != None:
timeStamp_name_l = list(timeStamp.keys())
timeStamp_l = [pd.Timestamp(x) for x in list(timeStamp.values())]
# 准备通用关键时间点时间戳
time_max = timeSeries.max()
time_min = timeSeries.min()
time_now = pd.to_datetime(datetime.datetime.now().strftime('%Y-%m-%d %H:%M:%S'))
timeStamp_name_l.extend(['time_max', 'time_min', 'time_now'])
timeStamp_l.extend([time_max, time_min, time_now])
# 时间差特征衍生
for timeStamp, timeStampName in zip(timeStamp_l, timeStamp_name_l):
time_diff = timeSeries - timeStamp
features_new['time_diff_days'+'_'+timeStampName] = time_diff.dt.days
features_new['time_diff_months'+'_'+timeStampName] = np.round(features_new['time_diff_days'+'_'+timeStampName] / 30).astype('int')
if precision_high != False:
features_new['time_diff_seconds'+'_'+timeStampName] = time_diff.dt.seconds
features_new['time_diff_h'+'_'+timeStampName] = time_diff.values.astype('timedelta64[h]').astype('int')
features_new['time_diff_s'+'_'+timeStampName] = time_diff.values.astype('timedelta64[s]').astype('int')
colNames_new = list(features_new.columns)
return features_new, colNames_new
# 测试函数使用
t = pd.DataFrame()
t['time'] = ['2022-01-03;02:31:52',
'2022-07-01;14:22:01',
'2022-08-22;08:02:31',
'2022-04-30;11:41:31',
'2022-05-02;22:01:27']
timeStamp = {'p1':'2022-03-25 23:21:52', 'p2':'2022-02-15 08:51:02'} # 关键时间戳,起始时间
features_new, colNames_new = timeSeriesCreation(timeSeries=t['time']
,timeStamp=timeStamp # 手动输入的关键时间节点的时间戳
,precision_high=True) # 是否精确到时、分、秒
# 时间精度更低一级的时序特征衍生,时分秒一般用不上
features_new, colNames_new = timeSeriesCreation(timeSeries=t['time']
,timeStamp=timeStamp # 手动输入的关键时间节点的时间戳
,precision_high=False) # 是否精确到时、分、秒
# 不添加关键时间戳
features_new, colNames_new = timeSeriesCreation(timeSeries=t['time']
,timeStamp=None # 手动输入的关键时间节点的时间戳
,precision_high=False) # 是否精确到时、分、秒













